An official website of the United States government
 United States Department of Labor
United States Department of Labor
A correction to this article was made on June 26, 2019. Specifically, the percent of workers projected to transfer occupations was changed to 6.4 percent. See https://www.bls.gov/bls/erratabydate.htm for more information.
The U.S. Bureau of Labor Statistics (BLS) produces 10-year employment projections, by occupation and industry, to help workforce development professionals and education providers understand the future composition of the labor market. These projections are also used by individuals making career decisions. In addition to projecting the number of new jobs to be created, BLS estimates a broader measure of future job availability, which includes the projected number of occupational separations. The total number of occupational openings is the sum of three components: occupational growth, occupational transfers (e.g., an accountant becoming a manager), and labor force exits (e.g., a worker retiring). Collectively, occupational transfers and labor force exits are known as “separations,” and they are the primary driver of job openings.
For the 2016–26 period, BLS projects that, each year, 4.7 percent of workers will leave the labor force and 6.4 percent will switch occupations, on average. These rates vary widely across occupations, not only because the occupations are different but also because their workers differ by demographic characteristics (e.g., age and educational attainment). Using figures from the 2016–26 projections, this article explores the effects of a worker’s demographic characteristics on his or her propensity to leave the labor force or transfer to a different occupation. Although each characteristic can be associated with a range of effects, two factors—age and education—are typically the largest contributors to a worker’s propensity to leave the labor force or change occupations.
BLS calculates separation rates by modeling the labor market participation of individual respondents to the Current Population Survey (CPS).1 Two probit regression models are developed: one for labor force exits and another for occupational transfers.2 These models allow BLS to estimate the probability that an individual will leave the labor force or transfer to a different occupational group. This probability is then used to calculate the number of labor force exits and occupational transfers expected in each occupation.
The two models are as follows:
prob(exit) = f(age, sex, age·sex, occupation, education, occupation·education, race, ethnicity, citizenship, full-time status, class of worker, industry, year)
prob(transfer) = f(age, sex, occupation, education, occupation·education, race, ethnicity, citizenship, full-time status, class of worker, industry, year)
The model of labor force exits includes all of the variables in the occupational transfers model, as well as the interaction of age and sex (denoted as “age·sex” in the equation above). Both models treat all variables as categorical, so each model produces a set of coefficients corresponding to the possible levels of each variable. As a result, the sum of the coefficients associated with a worker’s characteristics is a z-score describing that worker’s probability of exiting the labor force or transferring to a different occupation. Because a change in a z-score does not equate to a specific change in probability, the relationships described by the coefficients suggest that a decrease (increase) in a z-score results in a lower (higher) probability of leaving the labor force or switching occupations.
As an example, table 1 presents the attributes of a randomly selected CPS respondent and their effects on the respondent’s z-scores.
| Attribute | Value | Effect on z-score | |
|---|---|---|---|
| Labor force exit | Occupational transfer | ||
Intercept | — | -0.95 | -2.68 |
Age | 55–59 | -0.67 | 0.40 |
Sex | Female | 0.06 | 0.00 |
(Age) × (Sex) | (55–59) × (Female) | 0.04 | — |
Occupation | Healthcare practitioner and technical occupations | -0.22 | -0.30 |
Education | Bachelor’s degree | -0.09 | 0.07 |
(Occupation) × (Education) | (Healthcare practitioner and technical occupations) × (Bachelor’s degree) | 0.01 | -0.33 |
Race | White | 0.00 | 0.00 |
Ethnicity | Non-Hispanic | 0.00 | 0.00 |
Citizenship | Native | 0.05 | 0.14 |
Full-time status | Full time | -0.36 | 0.13 |
Class of worker | Wage and salary | 0.00 | 0.23 |
Industry | Educational and health services | -0.03 | 0.04 |
Year | 2016 | 0.00 | 0.00 |
Total | — | -2.15 | -2.30 |
Source: U.S. Bureau of Labor Statistics and author's calculations. | |||
In total, the labor force exit model yields a z-score of −2.145 for this example worker. Consulting the standard normal distribution, we find that this z-score corresponds to the worker having a 1.6-percent chance of leaving the labor force within a 9-month period.3 To convert this estimate to an annual rate, we multiply it by 12/9, obtaining a rate of 2.1 percent. The model calculations are as follows:
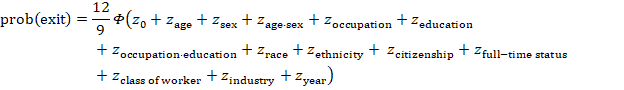
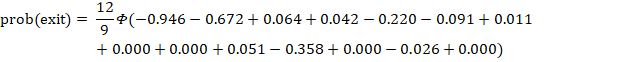
![]()
![]()
The same process is applied to the model of occupational transfers, yielding a probability of 1.4 percent that the worker will transfer to a different occupation. This example is revisited throughout the article, to explore how changes in attributes can affect a worker’s probability of leaving the labor force or changing occupations.
Although the BLS models of occupational separations include 13 components, the following analysis examines only those with the most notable effects, namely, age, sex, educational attainment, and major occupational group. These variables are not all independent in their effects on labor force exits and occupational transfers, so the BLS models include two composite variables to capture specific interactions: age·sex and occupation·education. Because of these interactions, the effects of age and sex are examined together, as are the effects of education and occupation.
All probabilities presented in subsequent figures and tables are calculated for the example worker introduced in the previous section. The calculations vary only the characteristics displayed in a figure or table.
The models of labor force exits and occupational transfers both include age and sex as variables. In addition, the composite variable age·sex is included in the labor force exits model. A worker’s age has the largest influence on his or her probability of leaving the labor force or transferring to a different occupation. The age·sex variable, which accounts for the sex-specific effects of age, has a strong influence on a worker’s probability of leaving the labor force. This interaction variable is not included in the model of occupational transfers because it was found to have no discernible effect on a worker’s probability of switching occupations. Sex alone does affect labor force exits and occupational transfers, but the effect is very small in both cases.
Workers in the youngest age groups have relatively high probabilities of exiting the labor force, but these probabilities decline over a period of 15–20 years. (See figure 1.) Men reach their lowest likelihood of exiting the labor force at ages 35 to 39, and women do so at ages 40 to 44. For both groups, the propensity to exit the labor force subsequently increases with age, as workers become more likely to retire or otherwise leave the labor force.
Although both sexes exhibit the same general trend, the age·sex variable allows the BLS model to account for male–female differences in the way age affects the probability of exiting the labor force. To illustrate this effect, we can calculate the example worker’s annual probability of leaving the labor force in each age group and for each sex, holding all other characteristics constant. Figure 1 shows that women exit the labor force at higher rates than men at all ages below 70. The male–female difference in labor force exit rates is greatest between the ages of 20 and 39, when women exit the labor force at much higher rates than men.
The model of occupational transfers is slightly simpler, because it does not include the age·sex variable. As in the model for labor force exits, age is the largest contributor to a worker’s likelihood of transferring to a different occupation. This likelihood peaks at ages 18–19 and then declines continuously with age. (See figure 2.) In all cases, men are slightly more likely than women to change occupations.
The models of labor force exits and occupational transfers both include variables for educational attainment and major occupational group. In addition, the models include a composite variable—occupation·education—which accounts for the occupation-specific effects of educational attainment. This variable shows the differential rates of labor force exit, by level of education, of similar workers in a given occupation.
Table 2 shows that occupation, education, and occupation·education each contribute to the example worker’s likelihood of exiting the labor force. In this case, the worker has a bachelor’s degree, and her annual probability of exiting the labor force is 2.1 percent. However, if the worker had a doctoral degree, she would have the values shown in table 3. Here, the net effect of the three variables is an even lower likelihood of exiting the labor force, 1.2 percent.
| Attribute | Value | Effect on z-score, labor force exit |
|---|---|---|
Occupation | Healthcare practitioner and technical occupations | -0.22 |
Education | Bachelor’s degree | -0.09 |
(Occupation) × (Education) | (Healthcare practitioner and technical occupations) × (Bachelor’s degree) | 0.01 |
Source: U.S. Bureau of Labor Statistics and author's calculations. | ||
| Attribute | Value | Effect on z-score, labor force exit |
|---|---|---|
Occupation | Healthcare practitioner and technical occupations | -0.22 |
Education | Doctoral degree | -0.03 |
(Occupation) × (Education) | (Healthcare practitioner and technical occupations) × (Doctoral degree) | -0.26 |
Source: U.S. Bureau of Labor Statistics and author's calculations. | ||
As these examples show, higher levels of educational attainment are generally associated with lower probabilities of exiting the labor force. In most occupational groups, this trend continues across the spectrum of educational attainment. (See figure 3.1.)
In a few cases, however, the labor force exit rate is lowest for workers with a master’s degree and increases for workers with a doctoral degree. (See figure 3.2.) These cases may reflect malemployment, a situation in which a worker’s occupation is not commensurate with his or her educational attainment. As shown in the next section, some of the occupational groups exhibiting this trend are also among those with the highest rates of occupational transfers for workers with doctoral degrees.
In most occupational groups, higher levels of educational attainment are associated with either an increase or little change in a worker’s probability of transferring to a different occupation. As shown in figure 4.1, this is especially true for workers with education beyond high school, indicating greater occupational mobility for those with higher levels of educational attainment.
Just as some doctoral degree holders deviate from the general pattern for labor force exit rates, some doctoral degree holders deviate from the general pattern for occupational transfer rates. (See figure 4.2.) In these cases, occupational mobility is lower for those with doctoral degrees, likely because of the highly specialized nature of their education. Workers in legal occupations and healthcare practitioner and technical occupations make up the vast majority of such cases.
The BLS separations models account for a broad range of workers’ characteristics. Generally, age and educational attainment are among the strongest determinants of a worker’s probability of transferring to a different occupation or exiting the labor force. In addition, these two characteristics affect the models of labor force exits and occupational transfers in opposite ways. As workers age, they generally become more likely to leave the labor force and less likely to transfer to a different occupation. On the other hand, workers with greater educational attainment are typically less likely to leave the labor force and more likely to change occupations. In some occupational groups, however, workers with doctoral degrees break from these patterns.
Andrew O'Bar, "What’s behind occupational separations?," Monthly Labor Review, U.S. Bureau of Labor Statistics, June 2019, https://doi.org/10.21916/mlr.2019.13
1 Although BLS uses 10 years of CPS data to construct the separations models, some groups still have small sample sizes, which can contribute to extreme coefficients. Because BLS calculates separation rates by applying the separations models to each individual in the base-year data, individuals with rare characteristics have little effect on the published separation rates. Two examples of these uncommon cases include workers in legal occupations with educational attainment of less than a high school diploma and workers in farming, fishing, and forestry occupations who have doctoral degrees.
2 For more details on the models, see Michael G. Wolf and C. Brett Lockard, “Occupational separations: a new method for projecting workforce needs,” Monthly Labor Review, May 2018, https://doi.org/10.21916/mlr.2018.12.
3 The BLS separations models measure the changes in labor force status between the fourth and fifth interviews of the CPS. The period between the two interviews is 9 months (see https://www.bls.gov/opub/hom/cps/design.htm#rotation-of-the-sample).